Blog Post

Contextures: The Mechanism of Representation Learning

Runtian Zhai, PhD Dissertation
Computer Science Department, Carnegie Mellon University
zhairuntian at hotmail dot com
April 15, 2025
Paper Slides Poster

Estimated reading time: 20 min

Science of Representation Learning

Foundation models, very large models pretrained to be applied to a variety of downstream tasks, have achieved remarkable empirical success in recent years. Their success largely results from the scaling law, an observation that making models larger improves their performance on various tasks, and can also allow certain abilities to emerge. However, theoretical understanding of these models is quite limited. Specifically, two questions have not been answered to a satisfactory extent.

What representations do foundation models learn, and why are these representations useful for a variety of downstream tasks?
Can increasing the model size always improve the performance? If it cannot, how to make progress beyond the scaling law?

Answering these questions is crucial, especially at this moment when the field is rapidly evolving but scaling up models is seemingly producing diminishing returns. Many recently released models are not as impressive as their predecessors, such as GPT-4.5 versus GPT-4. Partially for this reason, at NeurIPS 2024, Ilya Sutskever predicted that "pretraining as we know it will end" (video). My belief motivating this work is that there is still room for progress in pretraining, but it requires a deeper understanding of the science of representation learning, which will facilitate the developement of the next generation of pretraining methods.

The Contexture Theory

My dissertation establishes the contexture theory. The central argument is that representations are learned from the association between two random variables: the input X and a context variable A. Here are some popular examples:

Learning Method	Input X	Context Variable A
Supervised learning	Sample	Label of X
Node embeddings on graphs	Node	Neighbor of X
Masked language modeling	Text	Masked version of X
Contrastive learning	Image	Cropped version of X
Vision-language models	Image	Text caption of X

The contexture theory is related to a concept in psychology called the two systems of thinking, proposed by psychologist Daniel Kahneman. The figure below illustrates this concept (source).

System-1 thinking is fast, automatic, and intuitive; examples include recognizing an image of a cat, calculating "2 + 2", and reciting one's own birthday. System-2 thinking is slow, deliberate, and analytical; examples include recognizing different breeds of cats, calculating "178 × 497", and determining if the next birthday is on Sunday. The contexture theory suggests that representation learning can do any type of system-1 thinking, as long as one can define X and A, and there is a sufficient amount of data. It can do system-1 thinking better than humans, thanks to their large memory and fast computation. This is a manifestation of Ilya Sutskever's deep learning hypothesis, which states that "If you have a large neural network, it can do anything a human can do in a fraction of a second." However, representation learning cannot do system-2 thinking, which is why foundation models today are still not as good as humans at reasoning, and teaching a model to reason usually requires more than just pretraining, such as reinforcement learning.

Mathematically, the association between X and A can be determined by their joint distribution P⁺(x, a). This P⁺ induces a linear expectation operator T_P⁺, which maps a function on A to a function on X. Specifically, for any function g(a), T_P⁺ maps g to f(x) = E_P⁺[g(A)|x]. For example, if A is the label of X, and g(a) is the label encoding of a, then (T_P⁺g)(x) is the encoding of the label of x.

As per functional analysis, under the Hilbert-Schmidt condition, we can do a singular value decomposition (SVD) on T_P⁺, which gives us a set of ordered singular values (called the spectrum), and the corresponding left and right singular functions. Left singular functions are functions of X, and right singular functions are functions of A. All the left singular functions form an orthonormal basis of the L² space on X, meaning that any f(x) can be represented as a linear combination of these functions.

Key result 1: The optimal d-dimensional encoder spans the same linear space as the top-d left singular functions of P⁺. We say that such an encoder learns the contexture of P⁺.

We call this linear space the top-d eigenspace. To get an intuition of why this result is true, we can make an analogy to principal component analysis (PCA). Let us suppose that there are only N possible values of X, and M possible values of A. Then, a function on X is essentially an N-dimensional vector, and a function on A is an M-dimensional vector. Since T_P⁺ is a linear operator, it is essentially an N-by-M matrix. Representation learning needs to learn a d-dimensional embedding E for the N possible values of X, so this E is an N-by-d matrix. PCA states that if E consists of the top-d left singular vectors of T_P⁺, then E is the optimal d-dimensional embedding, in the sense that it minimizes the reconstruction error.

Now let us explain why the encoder that learns the contexture is optimal in more details. The key is how we define the term "optimal". Obviously, no encoder is universally good. For any given encoder, one can adversarially construct a downstream task on which the encoder performs poorly. However, such adversarial tasks are usually irrelavant in practice. For example, in NLP, relevant tasks include sentiment analysis, translation, summary, question answering, etc. Counting how many words in a sentence contain the letter "e" is a valid task, but it is not what people would usually care about. In fact, LLMs today are poor on this task. The figure below is my interaction with Claude 3.7 Sonnet on April 28, 2025. Claude mistakenly thought that "baking" contains the letter "e", probably because its original form is "bake".

In reality, the encoder is only required to perform well on a tiny set of tasks, and an "optimal" encoder is defined to have a low worst-case error on this set of tasks. So how should we define this set of tasks? The prior knowledge we have is that the context should be useful for learning a predictor for the task. For example, if the context is given by randomly cropping images, then our prior knowledge is that the downstream labeling function should be invariant to random cropping. As such, we define a quantitative measure of how useful a context is for a task called compatibility. Then, we prove that the encoder that learns the contexture achieves the lowest worst-case approximation error on the set of all compatible tasks, and thus it is optimal. This also explains the essence of transferability in deep learning: it results from the compatibility between the pretraining context and the downstream task.

Now that we know which encoder is optimal, the next question is how to obtain the linear span of the top-d left singular functions. The conventional method is called kernel PCA, which involves eigen-decomposition of an m-by-m matrix, where m is the size of the dataset. The time complexity of kernel PCA is O(m³), which is not scalable to large datasets. Deep learning provides a faster way to do this. We can train a large model to optimize a variational objective R, such that R is optimized if and only if the encoder learns the contexture. Then, optimizing this R automatically gives us the optimal encoder.

Key result 2: The contexture can be learned by training a large model to optimize a variational objective.

In the paper, I prove that this method works for a lot of machine learning paradigms, such as supervised learning, contrastive learning, denoising autoencoders, generative models, etc.

Next, we discuss whether increasing the model size always improves the performance. The contexture theory implies that the answer is no.

Key result 3: Increasing the model size inevitably produces diminishing returns. Further improvement requires better contexts.

The intuition is that as we increase the model size, the function class of the encoder gets closer to the entire function space on X. As a result, the linear space spanned by the optimizer of R on this function class converges to the top-d eigenspace. When these two spaces are close enough, scaling up the model size will have little effect on the performance.

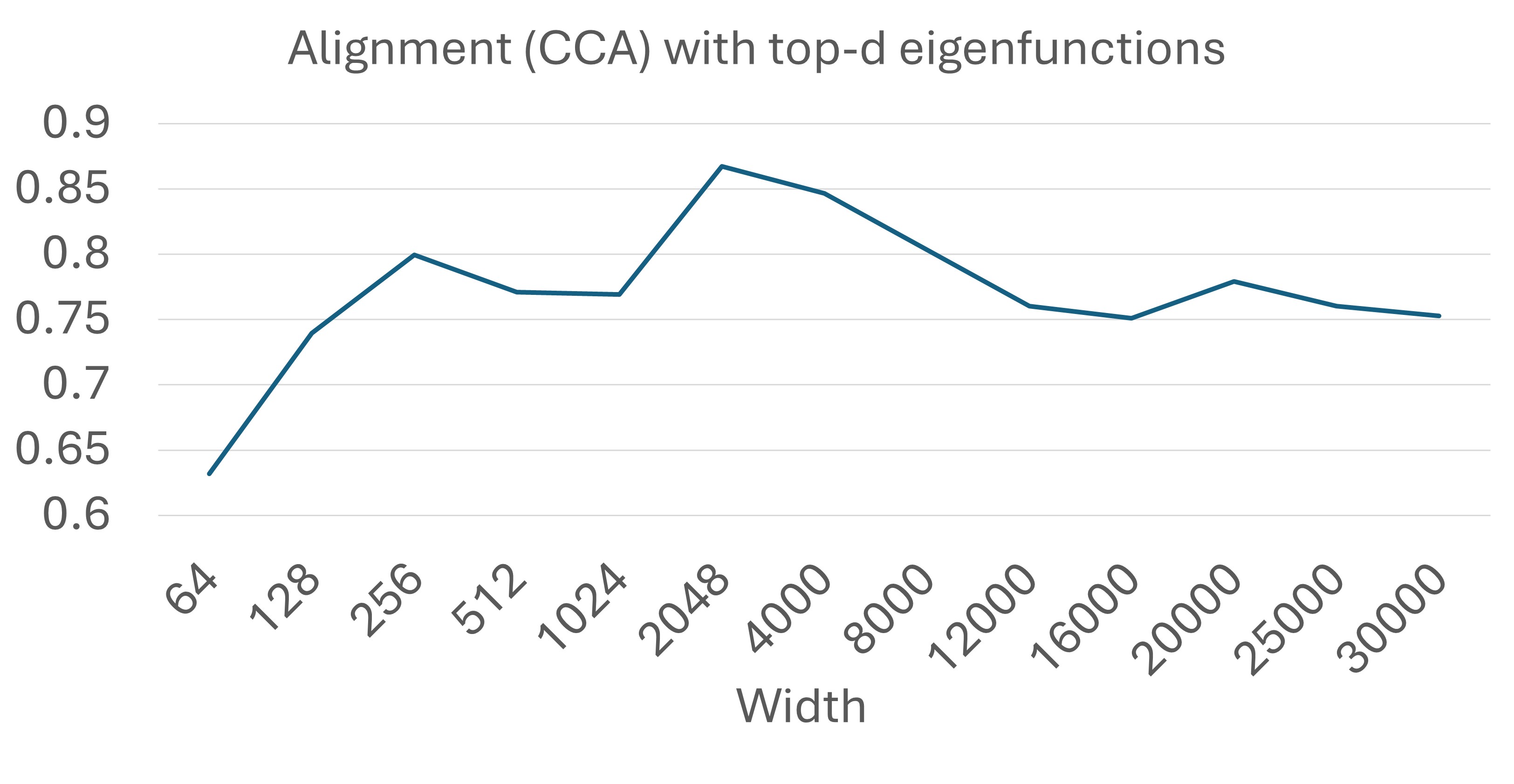
Here is an experiment that corroborates this intuition. Two encoders are trained on the same dataset. Encoder 1 consists of the exact top-d singular functions obtained by kernel PCA. Encoder 2 is an MLP trained by optimizing a variational objective. We measure the alignment between the two encoders using canonical correlation analysis (CCA). The result is shown in the figure below.

We fix the depth of the MLP to be 3 layers, and vary the width. When the model is sufficiently wide, the CCA can be higher than 0.85, which is considered a high alignment. However, further increasing the width could have a negative effect, probably because larger models are harder to train. Therefore, to make progress beyond the scaling law, we need to find better contexts.

Towards Better Contexts

The first thing we need to understand is which contexts are better. Better contexts lead to better encoders, so it depends on how we evaluate an encoder. There are two ways: Extrinsic evaluation and intrinsic evaluation. Extrinsic evaluation evaluates an encoder by its performance on a specific downstream task, which is what we ultimately care about in practice. Intrinsic evaluation does not use any specific task. It is more useful for pretraining for two reasons: first, we might not know all the downstream tasks at pretrain time; second, we want the encoder to be transferable to a variety of tasks, so evaluating it on only one task is insufficient.

The key result of intrinsic evaluation is the following.

Key result 4: A good context should have a moderate association between X and A.

To see why, let us consider two clearly bad contexts. In the first context, A is a random variable independent of X. In the second context, A = X. Both contexts are useless because A does not provide additional information about X. We can see that in the first context, the association between X and A is too weak; while in the second context, the association is too strong.

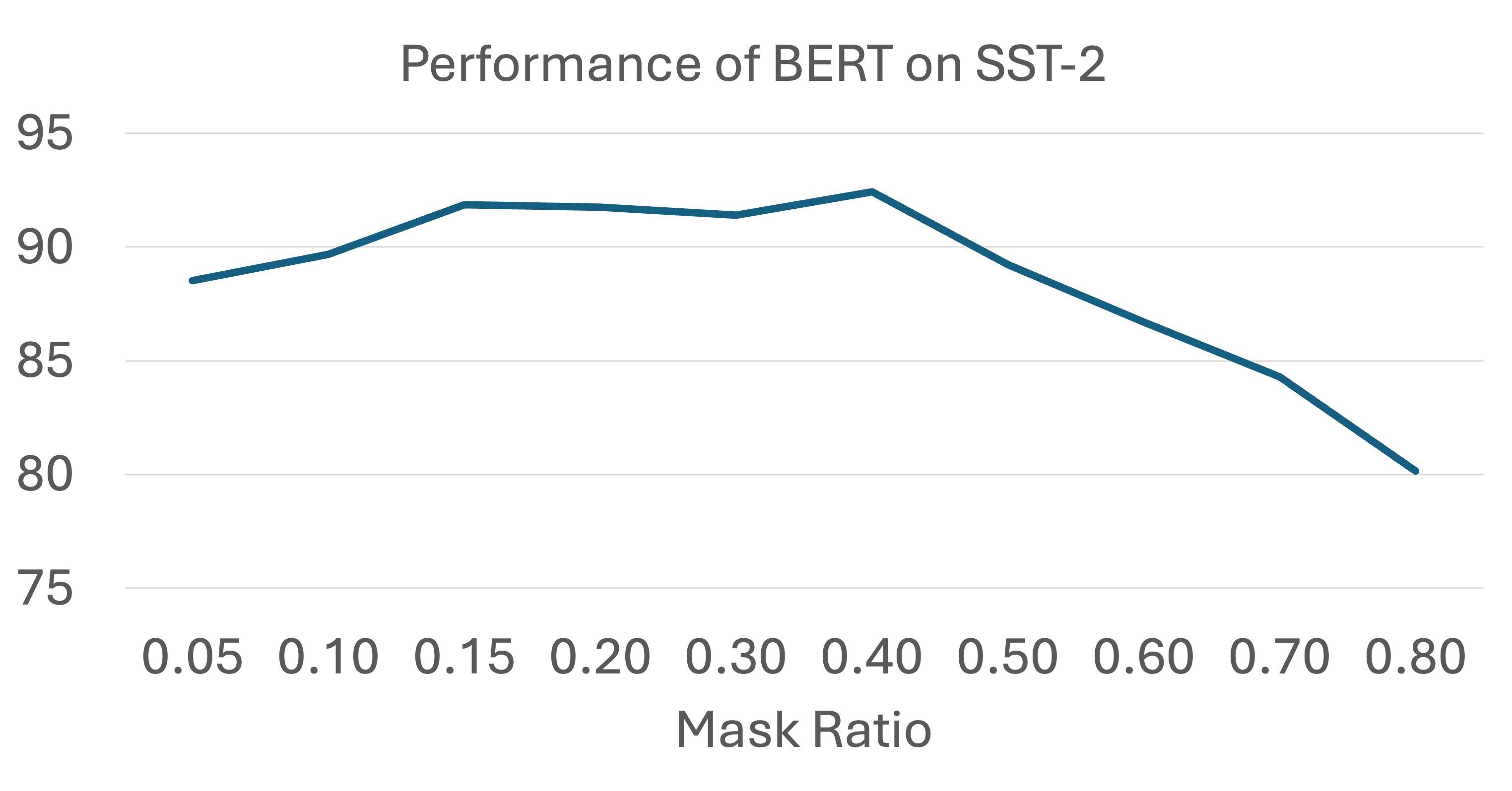
There is also abundant empirical evidence that a good context should have a moderate association. For example, a BERT has the best performance when the mask ratio is neither too high nor too low. The figure below plots the performance of BERT on the SST-2 downstream task as a function of the mask ratio. The performance is the highest when the mask ratio is around 0.4. When the mask ratio is too high, the association is too weak, and the pretraining task is too "hard" so that a good encoder cannot be learned. When the mask ratio is too low, the association is too strong, and the pretraining task is too "easy" and the information encoded in the task is insufficient.

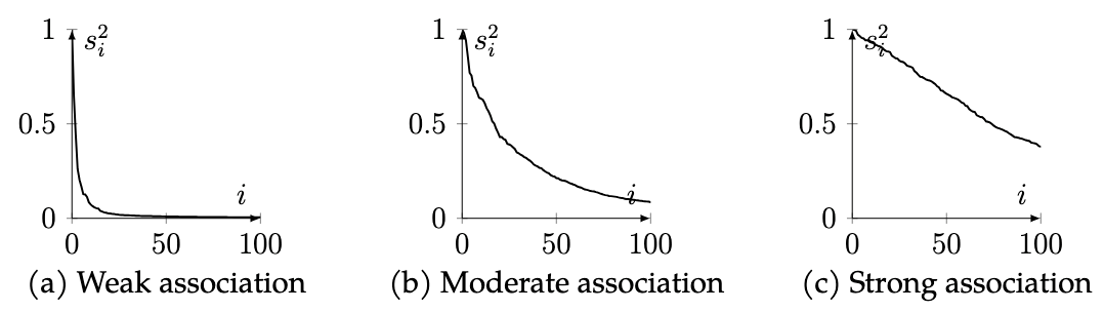
The association between X and A controls the shape of the spectrum, that is the decay rate of the singular values of T_P⁺. As illustrated in the figure below, when the association is weak, the spectrum decays fast. When the association is strong, the spectrum decays slowly. In the two extreme cases mentioned above, when A is independent of X, only the first singular value is 1 and all others are 0; when A = X, all singular values are 1.

The spectrum of a good context should decay at a moderate rate. In the paper, I also propose a metric to quantitatively measure this decay rate. The metric is large when the singular values decay too fast or too slow, and small when the singular values decay at a moderate rate. Therefore, this metric can be used to predict the downstream error of an encoder. I use experiments to show that this metric correlates well with the actual error on many real datasets.

Now suppose we have a number of different contexts, but none of them is good because the association of each of them is either too weak or too strong. In this case, we can mix them to form a better context with moderate association.

Key result 5: Mixing multiple contexts can lead to better contexts.

In the paper, I introduce three base operations for mixing contexts: convolution, convex combination and concatenation. The three operations should be used in different situations. Convolution is useful when all contexts have strong associations. Convex combination balances between strong and weak associations. Concatenation is useful when all contexts have weak associations.

Summary

In this dissertation, I propose a new theory of representation learning called the contexture theory. The theory provides a unified framework for understanding the mechanism of representation learning. It explains why representations are transferable, and why increasing the model size produces diminishing returns. The theory also provides a principled way to design better contexts, which is crucial for improving the performance of foundation models. I believe that the contexture theory is a step towards a deeper understanding of the science of representation learning, and it will help us develop the next generation of pretraining methods.

There are two directions I would like to pursue in the future. First, are generative models fundamentally different from embedding models on top of which a predictor is fit? In the paper I show that a generative model also learns the contexture of a certain context, but one key difference is that at inference time, generative models directly generate predictions instead of using a predictor. In this case, does the contexture theory still apply? Second, I would like to develop a theoretical framework for system-2 thinking, that is reasoning. Although recent LLMs have achieved impressive performance on many reasoning benchmarks, many people still doubt whether they are really capable of reasoning, instead of simply memorizing the answers. I envision that the theory for system-2 thinking will be fundamentally different from classical statistical learning theory, and even the contexture theory.